AutoSeM: Automatic Task Selection and Mixing in Multi-Task Learning

Guo et al. (NAACL 2019)

메인 과제의 성능을 높이는 보조 과제를 선정하는 문제를 1) task selection, 2) mixing ratio learning의 두 단계로 나누어 푼다. 1단계는 보조 과제의 집합을 고르는 Beta-Bernoulli multi-arm bandit을 푸는 단계로, 이 과정에서 Thompson sampling을 사용한다. 2단계는 고른 보조 과제들간의 미니배치 학습 순서와 횟수를 Gaussian process로 학습한다.

Framework

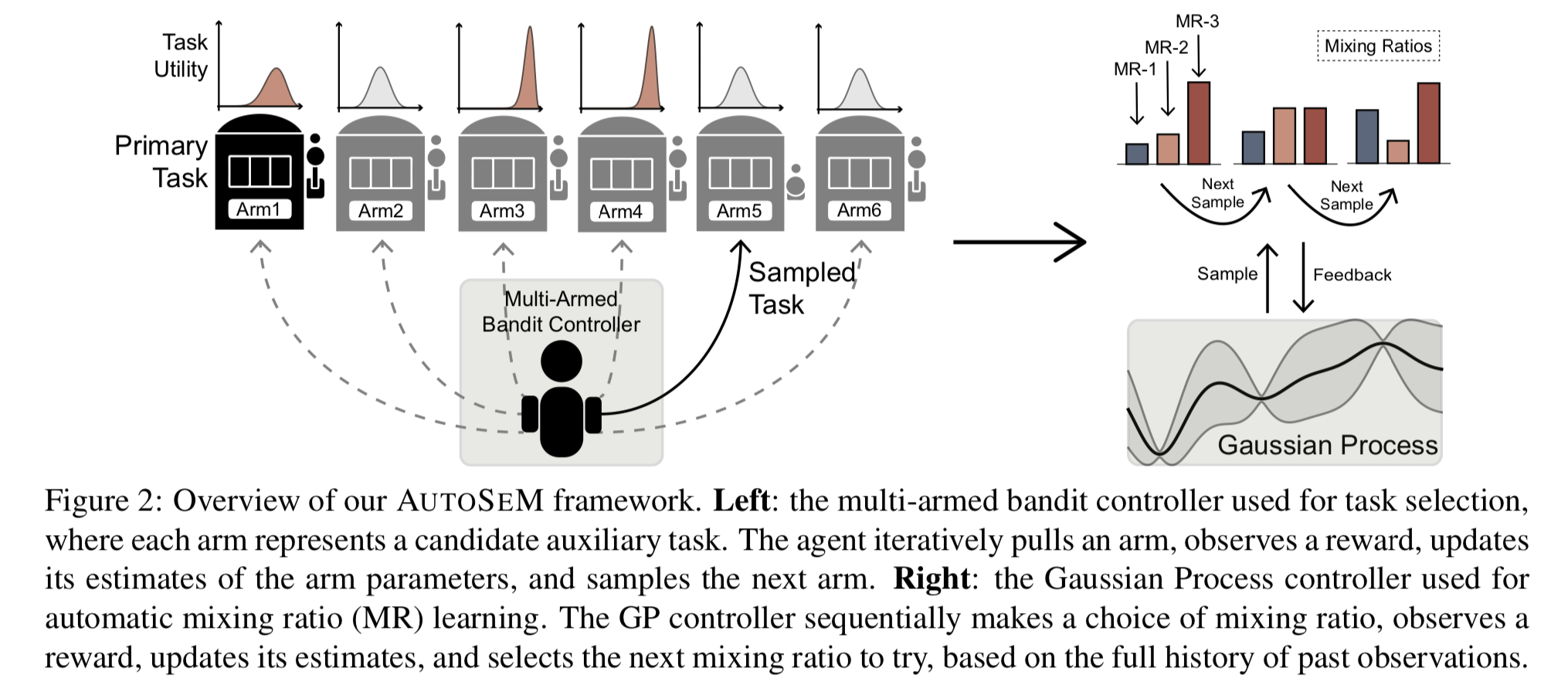
framework

1단계. Task selection

메인 과제도 하나의 arm으로 간주하여 여러 라운드에 걸친 multi-arm bandit을 푼다. 초반에는 메인 과제의 성능이 좋지 않으므로, 성능이 올라가는지 여부를 나타내는 utility가 overrate된다. 따라서 초반에는 메인 과제를 더 많이 샘플링하도록 strong prior를 주고, 메인 과제의 학습이 안정기에 접어들면 보조 과제를 많이 샘플링하도록 한다.

step1

Utility as Beta distribution. 어떤 과제 $k$ 에 대해서 round $t_b$ 에서의 reward $r_{t_b}$를, 이 과제 샘플링했을 경우 메인 과제의 validation metric이 오르는지에 대한 Bernoulli variable로 정의하자. 과제 $k$ 를 학습에 사용했을 때 reward 1을 발생시킬 확률, 즉 이 과제가 메인 과제의 성능을 향상시킬 확률을 utility $\theta \in [0,1]$ 이라 하자. 이에 대한 prior는 베타 분포로 나타낸다. Conjugacy에 의해 posterior도 베타 분포가 된다.

$\begin{aligned} p(\theta_k) &= \frac{\gamma(\alpha_k + \beta_k)}{\gamma(\alpha_k)\gamma(\beta_k)}\,\theta_k^{\alpha_k-1}(1-\theta_k)^{\beta_k-1} \\ p(\theta_k | r) &\propto \mathrm{Bern}_\theta(r)\,\mathrm{Beta}_{\alpha,\beta}(\theta_k) \\ &\propto \mathrm{Beta}_{\alpha+r,\beta+1-r} \end{aligned}$

Thompson sampling for exploration. 각 arm의 기댓값은 $\mathbb{E}_p[\theta_k] = \frac{\alpha_k}{\alpha_k + \beta_k}$ 인데, 기댓값의 argmax를 취해서 과제를 고르는 대신 posterior로부터 utility를 샘플링하여 ($\hat\theta_k \sim p(\theta_k |r)$) 이에 대한 argmax를 취하여 과제를 고른다.

Injecting non-stationarity. 어떤 과제가 유용한지 아닌지는 시간에 따라 바뀐다. 이것을 모델링하기 위해서 이전 관찰의 relevance를 줄이는 decay ratio $\gamma$ 를 사용하여 베타 분포의 파라미터를 업데이트한다.

$\begin{aligned} (\alpha_k, \beta_k) &= \begin{cases} (\hat\alpha_k, \hat\beta_k) + (r_{t_b}, 1-r_{t_b}) & \quad \text{if task k is sampled} \\ (\hat\alpha_k, \hat\beta_k) & \quad \text{else} \end{cases} \\ (\hat\alpha_k, \hat\beta_k) &= \left( (1-\gamma)\alpha_k + \gamma\alpha_0, (1-\gamma)\beta_k + \gamma\beta_0 \right) \end{aligned}$

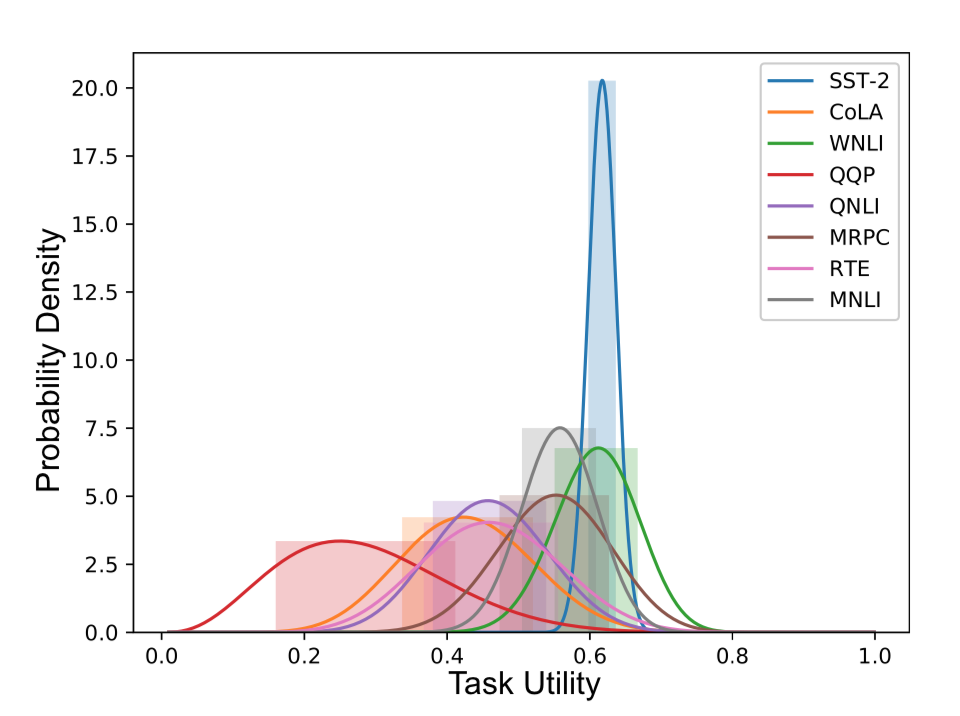step1Visualization 메인 과제가 SST-2일 때, 1단계의 결과 가우시안 분포로 나타나는 task utility의 예시.

2단계. Mixing ratio learning

Mixing ratio $\eta_1:\eta_2:\dots$ 는 첫번째 과제에 대해 $\eta_1$개의 미니배치를 보고 다음 과제로 넘어감을 나타낸다. 이것을 grid search로 찾는 것은 거의 불가능하기 때문에, non-parametric Bayesian approach인 GP를 사용한다.

Gaussian Process. $\mathrm{GP}(\mu_0, k)$ 는 mean 함수 $\mu_0$ 와 positive-definite kernel (covariance 함수) $k$ 로 표현된다. 랜덤한 초기 observation $\mathcal{D} = (\mathbf{x}_1, y_1), \dots, (\mathbf{x}_n, y_n)$ 를 설정하자. $\mathbf{x}_i$ 는 mixing ratio 하나에 해당되는 점이다. GP에서는 모델의 true performance $f(\mathbf{x}_i)$의 집합 $\mathbf{f} = {f_1, \dots, f_n}$ 이 joint Gaussian으로 상정된다: $\mathbf{f | X} \sim \mathcal{N}(\mathbf{m, K})$. 그렇다면, mixing ratio $\mathbf{x}_i$ 를 적용했을 때 관찰되는 (noisy) performance $y_i$ 는 $\mathbf{f}$ 를 mean으로 갖는 정규분포가 된다. $\mathbf{y|f} \sim \mathcal{N}(\mathbf{f}, \sigma^2\mathbf{I})$.

다음 mixing ratio point 샘플링하기. $x_{n+1}$ 을 GP에서 샘플링하여 $y_{n+1}$을 얻고 이 포인트로 GP를 업데이트한다. 샘플링 기준은 다음 세 가지 중에서 stochastic하게 고른다 (GP-Hedge approach).

Probability of improvement: $f(\mathbf{x}_{n+1})$ 이 현재까지의 max value보다 향상될 확률 (향상 크기는 무시)을 최대화하는 포인트를 고른다.
Expected improvement: 향상의 기댓값을 최대화할 포인트를 고른다.
Upper confidence bound: $\mu_i(\mathbf{x}_i) + \lambda\sigma_i(\mathbf{x}_i)$ 를 최대화할 포인트를 고른다.

모델

두 문장의 representation $\mathbf{u, v}$ 를 만드는 모델은 모든 task에 공유된다 (논문에서는 biLSTM + ELMo를 사용하였음). $\mathbf{h = [\,u; v; u \odot v; |u-v|\,]}$ 을 최종 representation으로 사용하며, 이것이 각 task의 projection 레이어로 통과되어 사용된다.

실험

Dataset: GLUE

메인 과제: RTE, QNLI, MRPC, SST-2, CoLA 중 하나.
보조 과제: Regression 과제인 STS-B를 제외한 나머지 (위의 것들 + QQP, MNLI, WNLI)
- 메인 과제가 단일 문장 분류일 경우 (SST-2, CoLA), 2문장 분류만 보조 과제로 사용

Results

1단계에서 Thompson sampling 결과로 top-2를 선정하고, utility threshold=0.5를 넘는 것을 추가로 선정.

MNLI가 모든 과제에서 유용하게 사용되었고 WNLI는 1단계에서 선정되더라도 2단계에서 기각되었다 (mixing ratio=0).

모두 baseline (biLSTM+ELMo) 대비 성능이 향상되었다.

RTE: QQP, MNLI (1:5:5)
MRPC: RTE, MNLI (9:1:4)
QNLI: (WNLI,) MNLI (20:0:5)
CoLA: MNLI, (WNLI) (20:5:0)
SST-2: MNLI, (MRPC, WNLI) (13:5:0:0)

bo-son